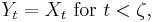Killed process
In probability theory — specifically, in stochastic analysis — a killed process is a stochastic process that is forced to assume an undefined or "killed" state at some (possibly random) time.
Definition
Let X : T × Ω → S be a stochastic process defined for "times" t in some ordered index set T, on a probability space (Ω, Σ, P), and taking values in a measurable space S. Let ζ : Ω → T be a random time, referred to as the killing time. Then the killed process Y associated to X is defined by
and Yt is left undefined for t ≥ ζ. Alternatively, one may set Yt = c for t ≥ ζ, where c is a "coffin state" not in S.
See also
References
- Øksendal, Bernt K. (2003). Stochastic Differential Equations: An Introduction with Applications (Sixth edition ed.). Berlin: Springer. ISBN 3-540-04758-1. (See Section 8.2)